| Tetrahedral bipyramid | ||
|---|---|---|
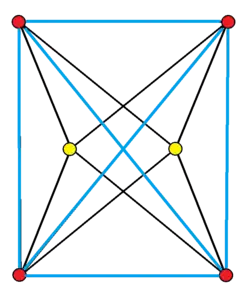 Orthogonal projection. 4 red vertices and 6 blue edges make central tetrahedron. 2 yellow vertices are bipyramid apexes. | ||
| Type | Polyhedral bipyramid | |
| Schläfli symbol | {3,3} + { } dt{2,3,3} | |
| Coxeter diagram | ||
| Cells | 8 {3,3} | |
| Faces | 16 {3} (4+6+6) | |
| Edges | 14 (6+4+4) | |
| Vertices | 6 (4+2) | |
| Dual | Tetrahedral prism | |
| Symmetry group | [2,3,3], order 48 | |
| Properties | convex, regular-faced, Blind polytope | |
In 4-dimensional geometry, the tetrahedral bipyramid is the direct sum of a tetrahedron and a segment, {3,3} + { }. Each face of a central tetrahedron is attached with two tetrahedra, creating 8 tetrahedral cells, 16 triangular faces, 14 edges, and 6 vertices,.[1] A tetrahedral bipyramid can be seen as two tetrahedral pyramids augmented together at their base.
It is the dual of a tetrahedral prism, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , so it can also be given a Coxeter-Dynkin diagram,
, so it can also be given a Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , and both have Coxeter notation symmetry [2,3,3], order 48.
, and both have Coxeter notation symmetry [2,3,3], order 48.
Being convex with all regular cells (tetrahedra) means that it is a Blind polytope.
This bipyramid exists as the cells of the dual of the uniform rectified 5-simplex, and rectified 5-cube or the dual of any uniform 5-polytope with a tetrahedral prism vertex figure. And, as well, it exists as the cells of the dual to the rectified 24-cell honeycomb.
See also
- Triangular bipyramid - A lower dimensional analogy of the tetrahedral bipyramid.
- Octahedral bipyramid - A lower symmetry form of the as 16-cell.
- Cubic bipyramid
- Dodecahedral bipyramid
- Icosahedral bipyramid
References
- Klitzing, Richard, "Johnson solids, Blind polytopes, and CRFs", Polytopes, retrieved 2022-11-14